Smackdown Revisited

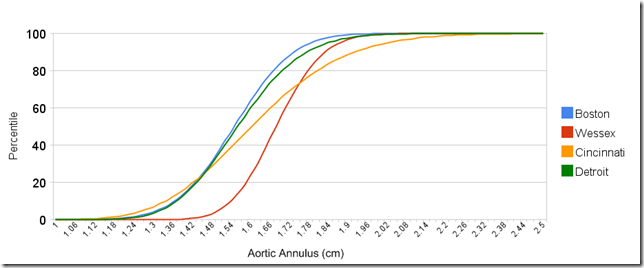
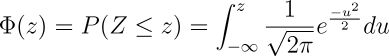After tackling the z-score:percentile issue, I thought it might be interesting to graph how different z-score equations look in this light. Here is what I derived as the cumulative density function for the aortic valve z-score (1.0 m²; male) using data published from Boston, Wessex, Cincinnati, and Detroit:

I think that because I have explained z-scores to our students and fellows so many times, and made use of my own roughly drawn bell-shaped curve, this next depiction of the probability density function highlights the differences most strikingly for me:

The mean (50th percentile) of the Wessex data is clearly and importantly different than the others... and only the Cincinnati data demonstrates an appreciable degree of skewness, with a long right tail. Of course, none of the investigators mention how they tested for skewness (mean/median/mode?).

(This post is an elaboration of an earlier comparison of different published z-score equations that graphically depicted the predicted mean values of the aortic valve annulus.)

---

Validation and re-evaluation of a discriminant model predicting anatomic suitability for biventricular repair in neonates with aortic stenosis.

Colan SD, McElhinney DB, Crawford EC, Keane JF, Lock JE.

J Am Coll Cardiol. 2006 May 2;47(9):1858-65. Epub 2006 Apr 17.

Relationship of the dimension of cardiac structures to body size: an echocardiographic study in normal infants and children.

Daubeney PE, Blackstone EH, Weintraub RG, Slavik Z, Scanlon J, Webber SA.

Cardiol Young. 1999 Jul;9(4):402-10.

Two-dimensional echocardiographic valve measurements in healthy children: gender-specific differences.

Zilberman MV, Khoury PR, Kimball RT.

Pediatr Cardiol. 2005 Jul-Aug;26(4):356-60. Erratum in: Pediatr Cardiol. 2008 Mar;29(2):475.

Regression equations for calculation of z scores of cardiac structures in a large cohort of healthy infants, children, and adolescents: an echocardiographic study.

Pettersen MD, Du W, Skeens ME, Humes RA.

J Am Soc Echocardiogr. 2008 Aug;21(8):922-34. Epub 2008 Apr 11.

Echo Z-Scores and Percentiles

I recently revisited the idea of calculating percentiles in addition to z-scores for the pediatric echo z-score calculators.

The cumulative percent is shown along with the z-score in the following image:

 

Since the relationship between z-score and percentile is constant, it seemed to me of no great benefit to add the percentile information. However, I now feel that percentiles convey information that some find more meaningful. For instance, the commonly accepted limits of normal for z-scores is -2 to +2 (the middle 95% of values). This range corresponds to percentiles of 2.3 and 97.7. But maybe a more realistic range of normal is

• 5th - 95th percentiles: z-scores of ± 1.65
• 10th - 90th percentiles: z-scores of ± 1.3

Using percentiles might encourage us to draw a more conservative boundary for the range of normal, which, in my opinion, will help us interpret otherwise "borderline" z-scores. Accepting the normal range of ±2, a z-score of -2.3 doesn't seem that far off. However, -2.3 is the 1st percentile- clearly nowhere near "normal".

---

Initially, I had thought that maybe I'd find a z-score/percentile table,  and simply incorporate a lookup routine,

but I like the idea of calculating the percentile better. However, the calculation (or rather, estimation) is hardly straightforward.

After some searching and trial and error, I finally found something that I could adapt. I admit I don't really understand how the polynomial approximation works, but hey, it does work, and it's in the public domain.

The first z-score calculator to receive the percentiles "upgrade" is the Aortic Root Z-Score Calculator. I hope to add the functionality to the others as well, as time permits.