Calculating Aortic Regurgitant Fraction

Using the echocardiographically obtained parameters of vena contracta width and abdominal aorta flow VTI’s to estimate the severity of aortic insufficiency.

The recent article An echocardiographic model predicting severity of aortic regurgitation in congenital heart disease presents an interesting model for predicting aortic regurgitation severity. Using MRI as their gold standard, the authors devised a “2 variable” model:

1. parasternal vena contracta area / BSA
2. abdominal aorta retrograde flow VTI / antegrade flow VTI

The mathematics-statisitics-voodoo behind developing this model are way beyond me. However, the final model is not too convoluted and it seemed an interesting object for a JavaScript calculator:

AR Fraction Calculator

Prototyping A Simple Database for Pediatric Echo Normal Values

A mashup of Google technologies to create a free, simple, open-access database.

The upcoming ASE Guidelines ”Recommendations for Quantification Methods During the Performance of a Pediatric Echocardiogram”, is intended to serve as The Standard for measurement techniques in pediatric echo. Getting everyone on the same page as far as making measurements is a prerequisite for moving forward with standardizing z-scores for pediatric echocardiography. Anticipating the guidelines, I built a mashup that could serve as a skeleton for a common database of normal values:

Normal Values Database Prototype: The Aortic Root

The above link is to a “working demo”. Feel free to enter any kind of data (fake or otherwise) in order to see it in action. Should I decide to do this “for real” there would likely be some preconditions for using the data form(s) but for now, feel free to use it with abandon.  Of course, I’d love to know what you think.

Kawasaki Disease Aneurysm Z-Scores: Another Smackdown

Boston Children’s versus Children’s National Medical Center for a “giant” knockout

When the Children’s National (CNMC) coronary artery z-score equations were published in 2008, I briefly compared them to the 2007 Boston data and noted their similarities. In my opinion, the manner in which the CNMC equations handle the “standard deviation” makes these incompatible with some newly proposed cutoffs. Let me explain.

Classifying Aneurysms

The current AHA criteria for classifying coronary artery aneurysms relies on a combination of z-scores and absolute diameters:

• any segment with a z-score of > 2.5 = abnormal
• <5 mm = small
• 5 – 8 mm = large
• ≥8 mm = giant

A recent article by Manlhoit et al. points out the folly of using absolute measurements in this instance. They then take the logical next step by introducing a classification system based on z-scores. Using their previously published data (from Boston, see above), the authors advocate the following coronary artery aneurysm z-score classification:

• ≥2.5 – <5 = small
• ≥5 – <10 = large
• ≥10 =  giant

The clinical science behind establishing these cutoff points is presented in the article and is beyond the scope of what I am trying to do here. However, it is worth noting that (at least to me) the proposed system has a certain elegance and symmetry— it just seems reasonable.

Z-Score Equations

The Boston and CNMC equations each predict very similar values for the BSA adjusted mean diameter by using an allometric model. The two equations also yield similar results out to about z-scores of +2. But the similarities end where coronary artery abnormalities begin. Using the new criteria proposed for giant aneurysms ( z ≥10 ) and applying the CNMC equations, patients who previously had giant aneurysms ( ≥8 mm) now only have large aneurysms.

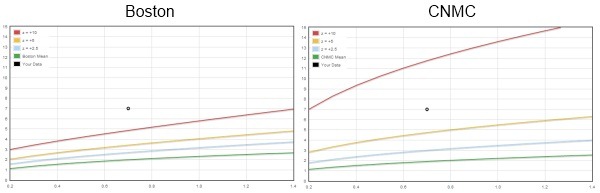
(See this page for the interactive comparison)

The big difference between the two z-score equations (z = [score – mean] / standard deviation ) is in how they deal with the standard deviation. The Boston equations use a separate regression (on BSA) to predict the SD, while the CNMC equations use the regression mean square error (MSE) statistic as a substitute for the SD.

Residuals

I have always been bothered by the patent substitution of the regression MSE (usually, the square root of the MSE i.e., the RMSE) for the population SD— particularly for the purpose of calculating z-scores. While the “transform both sides” strategy is perfectly legitimate for stabilizing the variance (and indeed, for discovering the allometric relationship!), if you play around with the regression residuals and then back-transform (i.e., exponentiate) your calculations — you have just modeled positive skew.

Detecting skew shouldn’t be all that hard to do. If the values are distributed normally, then it stands to reason that the residuals (observed - predicted) are also normally distributed. A simple plot of the residuals should show us what is going on. Here is the frequency vs. residuals plot from the recent fetal echo reference values of Lee et al.:

 

(Similar residuals plots are provided by the crazy-cool online curve fitting at ZunZun.com.)

That’s not to say that skew doesn’t exist. Indeed, that is part of the point and elegance of the recently applied LMS method. It is imperative that we do something to examine the presence or absence of skew, and then describe how we intended to deal with it. Unfortunately, both of these investigations fail to mention this fundamental data characteristic in their respective manuscripts.

Bottom Line

Due to unexplored assumptions about the nature of the residuals/skew of the data, z-score cutoff values are not universal and are absolutely dependent upon their underlying reference z-score equations.

Aortic Root Z-Scores part deux

A new z-score calculator for the aortic root (annulus, sinuses of valsalva, sinotubular junction, ascending aorta) is now available at ParameterZ.com.

In addition to the online z-score calculator I have also created:

• an example calculation walk-through
• a sinuses of valsalva z-score comparison
• an ascending aorta z-score comparison

Caveats

A couple of things worth mentioning as far as methodology:

1. Measurement of the sinuses/st jct., AAO are in diastole
2. Measurements are taken from leading edge - leading edge

The authors claim that these are in accordance with The Guidelines, yet they seem like a break in convention to me.

Adjusting for size

A recent article includes a cameo appearance by none other than ParameterZ.com:

Method 5: z-scores of LVM indexed for height^2.7 were calculated as described in a recent publication which is accessed using an online calculator at http://parameterz.blogspot.com/2008/09/lv-mass-z-scores.html (accessed 6 April 2009).

Incidence of left ventricular hypertrophy in children with kidney disease: impact of method of indexation of left ventricular mass.

Simpson JM, Savis A, Rawlins D, Qureshi S, Sinha MD.

Eur J Echocardiogr. 2009 Dec 15.

 

Unfortunately, the citation is not quite correct. The attribution is for “z-scores of LVM indexed for height^2.7" and, well, they are not. The z-scores are LV mass for height, to be sure, but not indexed for height. The authors assure me this was an error on their part and are going to issue a correction. The conclusions of their study remain unaffected by the mis-wording:  different methods of indexation have a profound influence on the categorization of children with respect to LVH.

The term “indexed” in this sense is fraught with misconception. If a measurement is found to be related to body size and an adjustment for body size is attempted- in any form- some are likely to simplify the adjustment by describing the relationship as being indexed to [insert body size parameter here]. Other interpretations are (correctly) more literal, taking the term indexed to mean divided by [insert body size parameter here].  (Further adding to the confusion is the use of the term index in programming jargon to mean “position within an array”, the use of which I am certainly guilty of in the course of explaining how the calculators work).

Adding to this particular variety of confusion is the recent work of one of the co-authors of the Foster et al., work wherein they reverse their previous position and go ahead and officially index LVM/height^2.7 but further correct for age (which in its own way seems to correct for height i.e., very few babies are tall). Even more frustration is going to get heaped on the “don’t index stuff” camp by this upcoming JASE article: Predicting Heart Failure Hospitalization and Mortality by Quantitative Echocardiography: Is Body Surface Area the Indexing Method of Choice? The Heart and Soul Study.

I don’t intend to settle this debate. All I am doing with ParameterZ.com is trying to make the information accessible and building some programming skillz in the process. All I can say is read the disclaimer and take it to heart— I do.

All calculations must be confirmed before clinical use or diagnostic purposes by qualified medical professionals.

Doppler Normal Values for Prosthetic Valves

Searchable, sortable normal Doppler values for aortic and mitral valve replacements.

Around the echo lab we are politely referring to the recent JASE Guideline Recommendations for Evaluation of Prosthetic Valves as "the Beast". Both for the size of the article (40 pages!) as well as the onus of now having to perform a more exhaustive evaluation on our valve replacement patients. We were used to just imaging the valve motion, reporting peak/mean gradients, and that was that.

I have no intention here of commenting on the Guidelines per se— interested readers should familiarize themselves with the actual document. I do want to mention the appendices, however, as I saw an opportunity to contribute and improve on the published data. Well, not the data itself so much as access to the data.

The five pages of tabular data summarizing the bulk of knowledge of normal Doppler parameters for prosthetic valves should be immediately available to anyone performing/reading an echo on a patient with a prosthetic valve. This is, I am sure, the reason for publishing the data tables in the first place. An Old School approach would have us photocopy, laminate, and bind the Journal pages and then keep them in the echo lab in conspicuously useful places.

I sought to put these tables some place even more useful, and simultaneously make the information easier to sift through:

• Prosthetic Aortic Valves: Normal Doppler Values

• Prosthetic Mitral Valves: Normal Doppler Values

Try using the search box and sorting the data by clicking on the header columns.

NOTE: The data is straight from The Guidelines which is in turn adapted from other works. Please let me know if you find any discrepancies with the published data. If your particular valve/size is not listed, sorry.

New Fetal Echo Z-Score References

New fetal cardiac z-score equations from William Beaumont Hospital; new online calculator at OBSONO.org

Following up on their abstract from earlier this year, the group at William Beaumont Hospital in Royal Oak, Michigan produced what turns out to be the largest cross-sectional study of normative data for fetal cardiac measurements of all time:

Fetal echocardiography: z-score reference ranges for a large patient population.
Lee W, Riggs T, Amula V, Tsimis M, Cutler N, Bronsteen R, Comstock CH.
Ultrasound Obstet Gynecol. 2010 Jan;35(1):28-34.

Data from over 2700 normal pregnancies was used to construct z-score equations for the following fetal cardiac measures:

• LV minor
• RV minor
• Aortic annulus
• Pulmonary annulus
• Cardiac circumference

By way of comparison, the previous work from Royal Brompton used data from 130 normal pregnancies; the more recent "unpublished" equations from Boston are based on observations made on 232 normal pregnancies. This new data eclipses both of these studies by at least an order of magnitude. For the purpose of generating normative data, "n" is everything, so statistically speaking, this study is HUGE.

The William Beaumont z-score equations deal with the prediction of the standard deviation in a manner similar to that used by the Boston folks, by a separate regression, thus deliberately accounting and controlling for the natural spread of data (heteroscedasticity). And, for what has to be one of the first, if not only, time- the authors also present a beautiful frequency vs. residuals plot and convincingly demonstrate that their data conforms to a normal distribution- a predicate for all z-score comparisons.

To better examine the differences and similarities of the various z-score equations I provide these tools, allowing for side-by-side comparison of the predicted z-scores, mean values, and normal ranges:

Fetal Aortic Valve Z-Score Comparison

Fetal LV Minor Z-Score Comparison

The authors also provide their own online fetal cardiac z-score calculator ( one-upping ParameterZ.com by generating pretty z-score plots ! ) at  www.obsono.org.

---

Speaking from the perspective of a pediatric cardiac sonographer, I have to recognize and thank the authors of this study for doing the work that we cannot do. Those of us in pediatric cardiology do not see a high volume of unselected, normal pregnancies and thus could never generate this kind of normative data.