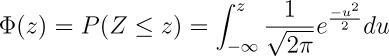I recently revisited the idea of calculating percentiles in addition to z-scores for the pediatric echo z-score calculators.
The cumulative percent is shown along with the z-score in the following image:
Since the relationship between z-score and percentile is constant, it seemed to me of no great benefit to add the percentile information. However, I now feel that percentiles convey information that some find more meaningful. For instance, the commonly accepted limits of normal for z-scores is -2 to +2 (the middle 95% of values). This range corresponds to percentiles of 2.3 and 97.7. But maybe a more realistic range of normal is
- 5th - 95th percentiles: z-scores of ± 1.65
- 10th - 90th percentiles: z-scores of ± 1.3
Using percentiles might encourage us to draw a more conservative boundary for the range of normal, which, in my opinion, will help us interpret otherwise "borderline" z-scores. Accepting the normal range of ±2, a z-score of -2.3 doesn't seem that far off. However, -2.3 is the 1st percentile- clearly nowhere near "normal".
Initially, I had thought that maybe I'd find a z-score/percentile table, and simply incorporate a lookup routine,
but I like the idea of calculating the percentile better. However, the calculation (or rather, estimation) is hardly straightforward.
After some searching and trial and error, I finally found something that I could adapt. I admit I don't really understand how the polynomial approximation works, but hey, it does work, and it's in the public domain.
The first z-score calculator to receive the percentiles "upgrade" is the Aortic Root Z-Score Calculator. I hope to add the functionality to the others as well, as time permits.