A Fortuitous Concatenation: Q and A with Frédéric and Nagib

The January issue of JASE holds this gem of a manuscript:

New equations and a critical appraisal of coronary artery Z scores in healthy children.
Dallaire F, Dahdah N.
J Am Soc Echocardiogr. 2011 Jan;24(1):60-74. Epub 2010 Nov 13.

The title couldn’t be any more fitting-- it is a must-read for anyone interested in the matter of z-scores for pediatric cardiology.

The authors have graciously agreed to allow me to post their answers to my “follow up questions”:

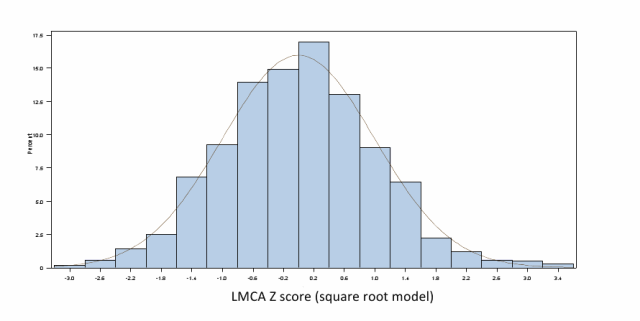
Q: Thanks for introducing us to the Anderson-Darling normal distribution test. However, why not include a few frequency vs. residuals histograms for the cavemen in the audience like me? We like pictures...: A: We used such histograms in our analysis to “visually” assess normality. Our article was however long and we had to cut down some of the text and figures. Here’s the frequency distribution for left main coronary artery Z scores (final model with square root of body surface area)
Q: Are there other normality tests? Why the Anderson-Darling test?: A: The Anderson-Darling test tests whether a sample fit to a given distribution. When used to test for departure from normality, it is one of the most powerful. SAS also gives the results for the Kolmogorov-Smirnov and Cramer-von Mises tests, which are less sensitive.
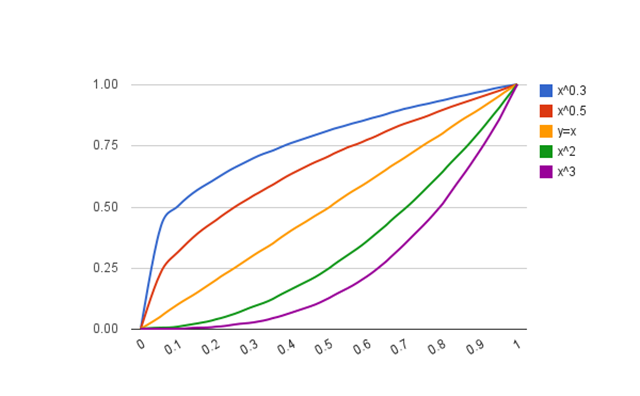
Q: The power model described in the article has the form: y = a +b₁x²+b₂x Why isn't that a polynomial model (quadratic)? I was expecting a model of the form: y : x^a(see chart).

Is this just a matter of semantics, or is the power model misnamed?: A: Yes, we should have named it a polynomial model.
Q: Judging by the spread/skew of the +/- 2SD curves on the “exponential model”, it looks like a log-normal curve... how did you treat the SD with this model?: A: In the exponential model, body surface area and coronary diameter were both log-transformed and then the model was fitted. The SD used was thus the one of a linear model on log-transformed values. Even with the logarithmic transformation, there was residual heteroscedasticity and a weighted least-square model was used. The weight in the model was the inverse of the linear regression of the residuals (on log-transformed values).
Q: Your “exponential model” empirically arrived at an exponent of 0.544-- similar to your theoretical “square root model”: y = a + b₁x^0.5. However, the Boston and Washington, D.C. models are similar and have exponents of something like 0.3xx. Is the difference between the exponents attributed to your larger sample size, or could there be something else going on here?: A: Hard to say. I would guess that aside from the greater sample size, it is likely the better representation of small children and infants that made the difference. If the theoretical model of optimal cardiovascular allometry proposed by Sluysmans and Colan in 2004 is true, it seems logical that a good representation of children from all ages helped to produce a “real-life” model close to the theoretical model proposed by Sluysmans and Colan.
Q: The final models described in the article are very similar in form to many of the z-score equations from Boston: 2 regression equations; one for the mean, one for the SD. However, the Boston equations predict the SD by a regression against BSA. Your SD equations are run against the square root of the BSA. How does one determine the best model for the variance?: A: The best model for variance should be determined in the same way the model for the mean is. That is, one should ensure that the residuals are free of a trend (no association should exist between the residual and the independent variable). In other words, there should not be an association between the residuals of the residuals and the dependent variable. This was verified for our data but was apparently not done in previous series, including Boston’s.
Q: I keep wondering: if we took a hundred patients with the same BSA, what is the mean/median/mode/min/max/distribution of those measurements? What does that curve look like? Had you considered using something like the “LMS” method to do a group-wise evaluation?: A: The use of a Z score assumes that the coronary diameters of x patients with a given BSA are normally distributed. In fact, our modelisation supposes that for any given value of BSA, there exists a number of subjects that are normally distributed around the mean (see our figure). If so, the median, mode and mean should be the same. The important thing is that in the absence of such a distribution, the Z score cannot be used to estimated percentiles, which is its principal (only?) value. In the lab, one wants to know if a coronary diameters exceeds the 95th or 98th percentile for a given BSA to be able to answer the question “is that coronary abnormal?”. Such percentiles can only be estimated if the data is normally distributed.
Q: What do you think explains how the proximal RCA has a normal distribution in your analysis but the distal RCA does not?: A: The distal RCA has two particularities. 1) distal RCA is the most difficult to view and, therefore, to measure. We are confident all distal RCA measurements we use to compute our equations were properly imaged and measured (number of distal RCA samples are the lowest compared to the other segments in our report). The difficulty of obtaining good image might have played a part, but we do not think this is the main reason for the non normal distribution... 2) Essentially, the size of the distal RCA depends on whether or not the RCA is dominant or not (typically 2/3 vs 1/3 of normal humans). We think this is the most probable explanation for not perfectly symmetric variability among subjects. In brief, we believe that the dominance factor is the key answer. One way to verify this hypothesis is to take the adventure of measuring the distal circumflex (posterior rim) and compare with the distal RCA in a series of subjects...
Q: If you consider coronary arteries as a microcosm of the larger reference values issue in pediatric cardiology, what implications does your work have for the existing body of z-score equations?: A: Surprisingly, very little proper validation of reference values and normalisation has been done in paediatric echocardiography. We advocate for a close examination (and potentially a redo when appropriate) of nearly all equations so far available in the literature. Some of them are probably adequate, but in the absence of a good description of the final distribution, it is difficult to affirm with confidence.
Q: Do you have any advice for others, like the ASE, that are going forward with developing new models and z-score equations?: A: Simply fitting a modelled curve in the data is not enough. Since Z scores are dependent on the distribution of the data, one should absolutely test the Z score distribution obtained. One should also ensure that there is no residual trend and no residual heteroscedasticity. We believe that Z scores are a very useful tool for interpreting cardiac structure dimensions in paediatric settings. They must however be based on sound unbiased mathematical grounds.