Scaling in Echocardiography: Psychosis

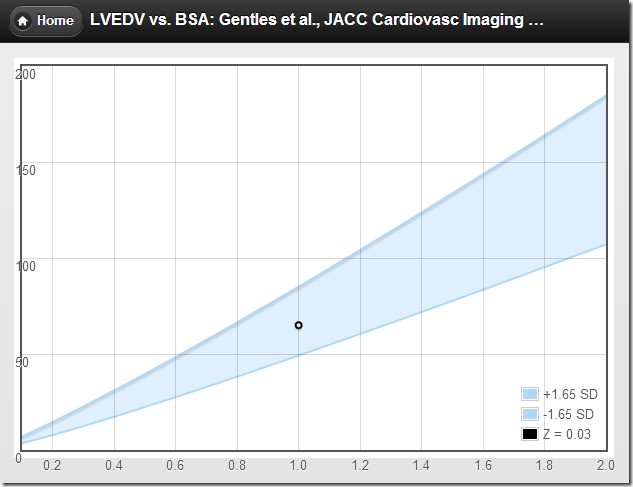
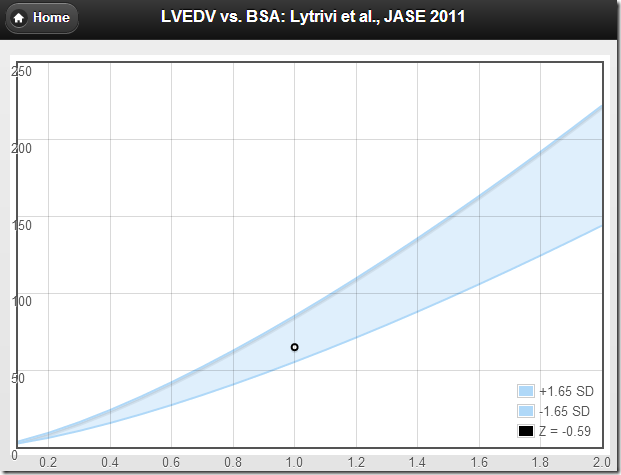
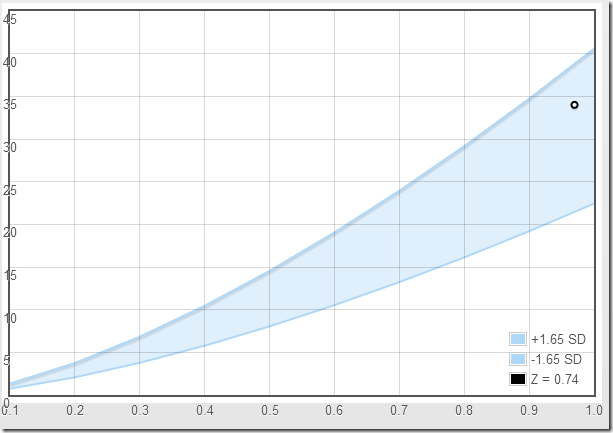
A recent editorial states “In terms of practicality, developing normative values of right-heart dimensions by indexing to BSA is an important first step and should be encouraged.” If by “encouraged” they mean “discouraged and abandoned” then I totally agree.

An editorial in the December JASE discusses recent additions to the body of knowledge concerning reference values for the right ventricle:

Editorial:

• Hoit BD.
  It's Time to Index the Right Ventricle, but to What and How?
  J Am Soc Echocardiogr. 2012;25(12):1277-9.

Recent articles:

• D’Oronzio U, Senn O, Biaggi P, Gruner C, Jenni R, Tanner F, et al.
  Right heart assessment by echocardiography: gender and body size matters.
  J Am Soc Echocardiogr. 2012;25(12):1251–1258
  
• Willis J, Augustine D, Shah R, Stevens C, Easaw J.
  Right ventricular normal measurements: time to index?
  J Am Soc Echocardiogr. 2012;25(12):1259–1267
  
• D’Andrea A, Riegler L, Morra S, Scarafile R, Salerno G, Cocchi R, et al.
  Right ventricular morphology and function in top-level athletes: a three-dimensional echocardiographic study.
  J Am Soc Echocardiogr. 2012;25(12):1268–1276

That reference values for the right ventricle need to be improved is undisputed. However, I think the editorial went awry and gave some of the authors an undeserved pass.

Firstly, as a matter of clarification, I believe the current guidelines for the right ventricle are unsuitable. Here’s why: they provide unscaled values:

In fact, the terms “scaled” and “body size” do not appear in the guideline document.
Anywhere.

Secondly, the editorial nicely details many of the shortcomings of indexing (i.e., heart size ÷ body size):

This approach is problematic for three reasons. First, the correlation between the cardiovascular parameter and body size may not be linear and may have unanticipated variation; second, difficulties may result when scaling a cardiovascular parameter to a body size parameter that has different dimensions (e.g., volume vs. area); and finally, it has been shown that ratiometric scaling does not produce size-independent scaled cardiovascular variables (i.e., the ratiometrically scaled variable (still) correlates with body size).

Yet the final assessment of the editorial is that indexed values are a “practical compromise”:

Indexing to BSA is a practical compromise but is inaccurate insofar as body composition affects the relation between body mass or surface area and cardiovascular variables; this problem may be particularly troublesome when normalizing dimensions in obese populations... In terms of practicality, developing normative values of right-heart dimensions by indexing to BSA is an important first step and should be encouraged.

There is some real truth in the problematic matter of using BSA as the size-adjusting parameter. The cardiovascular system has been optimized to deliver oxygen to tissues with a high metabolic need for it, i.e., lean body mass. Body surface area is a poor surrogate for LBM and, therefore, poorly represents the true relationship between body size, cardiac output, and organ size. But that is a problem for every attempt to scale heart size to body size, and not a unique problem for indexing. Indexing has it’s own flaws—fatal flaws—and couching those flaws in the terms of “BSA may be inadequate for obese populations” is misleading.

To be fair, the article by D’Andrea et al. understands the perils of indexing, and they should be recognized for their approach:

On the basis of the theoretical and empirical limitations of ratio scaling, we checked whether this scaling approach removed the influence of body size using a simple bivariate correlation approach. Where ratio scaling failed to remove the influence of body size, we subsequently investigated the nature of the allometric relationships between the BSA and 3D RV volumes and determined whether allometric scaling for the BSA provided size-independent RV dimensional indexes. Allometric scaling of the general form y = a * x^b was used.

 

---

In my opinion, the most rational piece of work covering the matter is the fantastic editorial, Does size matter? Clinical applications of scaling cardiac size and function for body size. It is so relevant to the topic, it was cited in the current editorial 4 times. However, those authors arrived at the entire opposite conclusion:

indiscriminate use of ratiometric scaling approaches is at best problematic and at worst dangerous...

Reliance on parameters ratiometrically scaled to BSA for clinical decision making should be discouraged.

What we need in echocardiography is something of a reality check...

Stay tuned for that:
A Review and Critique of the Statistical Methods Used to Generate Reference Values in Pediatric Echocardiography.

LVEDV Z-Scores

The second of two recent updates to app.parameterz.com is the addition of the left ventricular volume and dimension data supplied by this recent article:

Normalized end-systolic volume and pre-load reserve predict ventricular dysfunction following surgery for aortic regurgitation independent of body size.
Gentles TL, French JK, Zeng I, Milsom PF, Finucane AK, Wilson NJ.
JACC Cardiovasc Imaging. 2012 Jun;5(6):626-33.

(The equations are provided via an online supplement, supplied to me by the authors.)
Although the article describes equations for LV function and dimensions, I use only the dimensional z-scores. The form of these equations is that of an allometric relationship with BSA, with log-log transformation of both the measured value and the BSA.
The formula used for estimating BSA is not described within the article/supplement; I am awaiting a response from the authors on this. In the meantime, calculations are made using the Haycock formula.

LVEDD and LVESD

The allometric equations for the LVEDD and LVESD use exponents of around 0.4, which is slightly less than what would be expected by the theory of geometric similarity: 0.5. Numerous other authors have discovered linear relationships when correcting/adjusting linear dimensions (cm) to body surface area (m²). Additionally, the LVESD values seem a bit off when compared to other available sources:

(I have contacted the authors; awaiting their response)

LVEDV and LVESV

Data for the left ventricular volumes is also in the form of an allometric relationship with BSA, with an exponent of around 1.1. Again, this differs somewhat from what would be predicted by geometric similarity, and by other empirical evidence. The closer the exponent is to 1.0, the more the relationship is strictly linear with BSA, which is unexpected, particularly since the authors recognize this peril:

However, the relationship between body size and LV size is nonlinear

Yet, when you plot out the predicted values, it looks quite linear:

versus an allometric equation with an exponent of 1.38 (Lytrivi et al.):

Anyhow, given the paucity of ventricular volume z-score equations, these are now included among other pediatric echo z-score calculations at

app.parameterz.com

***update Dec 2012***

The author has advised me that there was an error with the online supplement.

"The intercept for ESD should be 2.56 NOT 3.56 as is on the web"

The app now uses the updated value.

Left Atrial Volume Z-Scores

Calculating BSA-adjusted z-scores of LA volume using an allometric equation
The first of two new calculations added to app.parameterz.com is based this recent article:

Normal values of left atrial volume in pediatric age group using a validated allometric model.
Bhatla P, Nielsen JC, Ko HH, Doucette J, Lytrivi ID, Srivastava S.
Circ Cardiovasc Imaging. 2012 Nov 1;5(6):791-6.

Similar to how this same group calculates z-scores for LV end-diastolic volume, they found an allometric equation that scales well with body size (in this case, two equations) and they index to that. For left atrial volume, there is one equation for BSA ≤ 1.0 and another equation for BSA > 1.0. The allometric exponent for the bigger kids, i.e., BSA^1.08, is not much different than just indexing to BSA, which strikes me as interesting.
I think the stratification into two groups would be more palatable if the interface was seamless, but in this case it is not. Let’s have a look at two patients with an LA volume of 34ml, one just under 1.0 meters squared and the other, just above.

1. BSA = 0.97; z = 0.74
2. BSA = 1.03; z = 1.65

And their accompanying plots:

BSA = 0.96

BSA = 1.03

For the smaller patient, the LA volume of 34 ml is well within the normal range, but for the slightly larger patient, the same LA volume is now at the upper limit of normal. Weird, huh?
Plus, it gets a little more interesting. If we assume that 125-131 cm is about the appropriate height for a 7 year old, and we plug the same data into another calculation, the indexed left atrial volume is definitely large, with a z-score of 3.5:

Anyhow (as always) I don’t pretend to have the answers— I just pose questions. Feel free to play around with this and other z-score calculations at:

app.parameterz.com

Fetal Tissue Doppler Z-Scores

Reference values and z-score calculations for fetal tissue Doppler E, A, and S waves added to new fetal echo z-score app.

I just wrapped up the design and implementation of a new fetal echo z-score site (fetal.parameterz.com) and as a test of the new modular design, I added the fetal tissue Doppler data from this recent article:

Gestational age- and estimated fetal weight-adjusted reference ranges for myocardial tissue Doppler indices at 24-41 weeks' gestation.
Comas M, Crispi F, Gómez O, Puerto B, Figueras F, Gratacós E.
Ultrasound Obstet Gynecol. 2011 Jan;37(1):57-64.

Although the article provides equations that adjust for fetal weight, since no pediatric cardiologist has ever asked me to estimate the fetal weight *wipes brow*, I have only included the gestational age-adjusted equations.

Jumping ahead for just a second, here is an example of the results page:

fetal tissue Doppler z-scores for a 28wk4d fetus

and here is an example chart:

fetal tissue Doppler LV TDI S vs. EGA

Challenges

Implementing a class that provided a common interface for calculating a mean, range, and z-score was non-trivial for this reference. There are no fewer than 5 distinct models that govern the E’, A’, and S’ calculations:

1. linear model with constant variance
2. linear model with non-constant variance
3. log-linear model with constant variance (log-normal)
4. log-linear model with non-constant variance (NOT log-normal ?)
5. log-polynomial model with non-constant variance (NOT log-normal?)

A second challenge was getting my calculations (based on the published data) to reconcile with the supplemental material (an Excel spreadsheet). In a few instances the spreadsheet used data with more significant digits than in the article, and in a few other instances the spreadsheet incorrectly exponentiates the “standard deviation” term. In the end, I figured that I had to go with the published data over the supplemental data. Also, it became clear after referring to the charts that the spreadsheet data was incorrect.

Concerns

Apart from the multiple models and the occasional inconsistency in the formulae, there is also the small matter of the article failing to provide the typical correlation coefficients for the models, and, therefore, necessarily omitting the “R-squared” values. The R² tell us about the goodness-of-fit or, sometimes, how much of the variance is explained by the model. For some of the dependent variables this seemed like an important omission as the models appear promising. I have included the data for the E’, A’, and S’ because they do look somewhat promising. I did not include the data for the derived values like the E’/A’,  E/E’ ratios or the MPI calculations because, to me, they seem dodgy—particularly without an R².

Summary

1. New fetal echo z-score calculator
2. New calculations for fetal tissue Doppler
3. I welcome your comments and criticisms

The Problem with Indexing Volumes to BSA

Wherein the inappropriate indexation of cardiac volumes to BSA is explored, this time with charts!




For some time now I have been aware of and abiding by the following words of caution:

linear dimensions and volumes have a nonlinear relation to surface area and
are more appropriately indexed by surface area to the 0.5 and 1.5 power, respectively.

-- Gutgesell and Rembold, Am J Cardiol. 1990

But since I work mostly with echocardiography and echocardiography has, mostly, gotten this message I haven’t explored the problem much. Recently though, I have been reading some of the cardiac MRI literature. Plus, it’s hard not to see some reference to CMR even in the echo literature. A lot of the CMR literature seem to use a cutoff for ventricular chamber enlargement like:
170 ml/m²
And, in the search for improving the sensitivity of echo, many study designs pit echo measures against CMR measures.
So what is the problem?
What are the consequences of an inappropriate index?

I put together a few charts that helped me to understand the real hazards of what sounds like a mostly theoretical problem—maybe they will be useful to others as well:

RVEDV vs. BSA

This chart shows the expected nonlinear relationship between RVEDV and BSA: the predicted values (grey) and the somewhat arbitrary z-score upper limit of +4 (red) are those of Buechel et al.; the conventional cutoff values of 170ml/m² are in yellow. Note that only at one place along the BSA spectrum is there an overlap of z-score and conventional indexed values: in this case, at somewhere around 1.7m² (a medium –sized adult). Moving away from that intersection, for BSA values lower than 1.7, it is increasingly likely that a measured RV volume will be interpreted as “below the cutoff value", yet exceed a z-score of +4.
For BSA values above approximately 1.7m², the reverse is true: it is increasingly likely that a measured RV volume will exceed the indexed cutoff value, yet fall below a z-score of +4.

Equivalent Z-Score for 170ml/m² vs. BSA

This chart shows the equivalent z-score (Buechel et al.) for the conventional cutoff values of 170ml/m² over the entire range of BSA.

The problem of using an inappropriately indexed value isn’t purely theoretical, and it isn’t just a matter of making it harder for echo researchers to find statistical significance—it is a matter of finding or, frankly, missing patients with important, real, abnormalities.

---